エクスプレッションビルダー マスファンクション 日本語訳
使用ソフト
- Lightwave2020
◇マスファンクション入門
このセクションに示されている数学関数は、代数と三角法で見つかるほとんどすべての標準的な数学関数を含んでいます。
これらの関数は、初心者から上級者までのためにここにリストアップされていますが、注意してください。これらの関数の使用方法を教えるのはエクスプレッションビルダーの範囲外です。
このセクションのほとんどで、「サンプル」と「アプリケーション」のタブにはほとんどテキストがないことに気づくでしょう。
これらの数学関数がどのように機能し、その理由を完全に理解するには、代数と三角法の教科書を参照してください。
2024,06,29 「Math Functions 101」の翻訳を追記
ファンクション
acos (Arc-Co-Sine)
◇記述( Description)
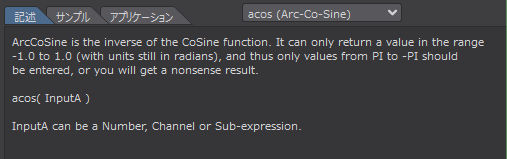
'ArcCoSine' は CoSine 関数の逆関数です。この関数は-1.0から1.0(単位はラジアンのまま)の範囲の値しか返せないので、Plから-Plまでの値しか入力してはいけません。
acos( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
asin (Arc-Sine)
◇記述( Description)
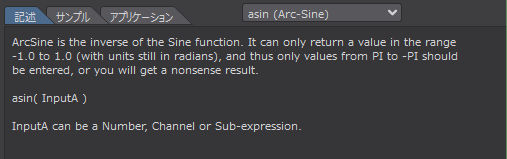
'ArcSine' はSine関数の逆関数です。この関数は-1.0から1.0(単位はラジアンのまま)の範囲の値しか返せないので、Plから-Plまでの値しか入力してはいけません。
asin( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
atan (Arc-Tangent)
◇記述( Description)
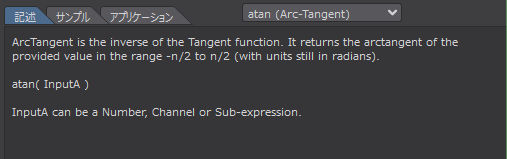
'ArcTangent' は Tangent 関数の逆関数です。入力された値のArcTangentを -n/2 から n/2 の範囲で返します(単位はラジアンのまま)。
atan( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
cos (Co-Sine)
◇記述( Description)
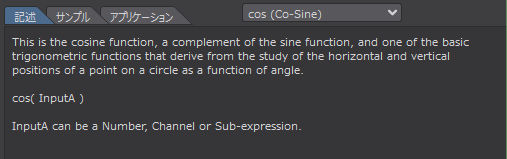
これは CoSine 関数で、Sine 関数の補数であり、円上の点の水平と垂直の位置を角度の関数として研究することから派生した基本的な三角関数の一つです。
cos( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
cosh (Hyperbolic-Co-Sine)
◇記述( Description)
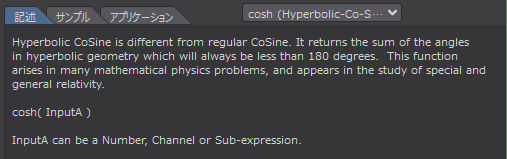
Hyperbolic CoSine*1は通常のCoSineとは異なります。
これは双曲幾何学の角度の和を返すもので、常に180度より小さくなります。
この関数は多くの数理物理学の問題で使われ、特殊相対性理論や一般相対性理論の研究にも登場します。
cosh( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
cot (Co-Tangent)
◇記述( Description)
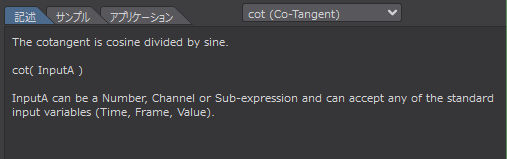
cotangentは CoSine を Sine で割ったものです。
cot( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
csc (Co-Secant)
◇記述( Description)
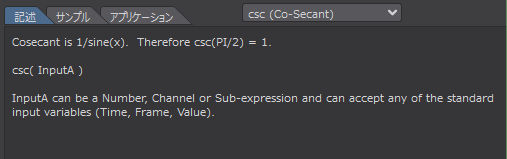
Cosecantは1/sine(x)です。したがって csc(PI/2) = 1.
csc( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
exp (Exponent)
◇記述( Description)
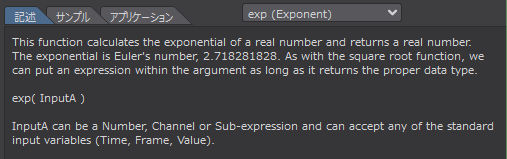
この関数は実数の指数を計算し、実数を返します。指数とはオイラーの数、2.718281828のことです。平方根関数と同様、適切なデータ型を返す限り、引数の中にエクスプレッションを入れることができます。
exp( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
log (Logarithm)
◇記述( Description)
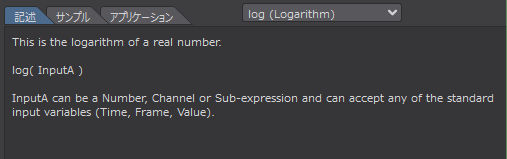
これは実数の対数です。
log( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
sec (Secant)
◇記述( Description)
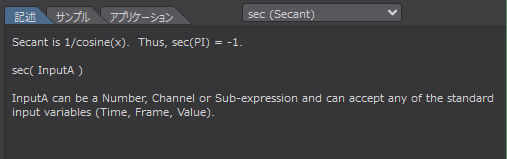
Secant*2 は 1/cosine(x) である。したがって、sec(PI) = -1。
sec( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
sin (Sine)
◇記述( Description)
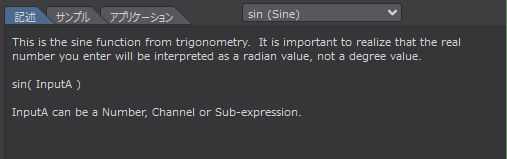
これは三角法*3のsin関数です。入力した実数は度数ではなくラジアン値として解釈されることを理解しておくことが重要です。
sin( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
sinh (Hyperbolic-Sine)
◇記述( Description)
Hyperbolic Sine(双曲線正弦)は通常の正弦とは異なります。これは双曲幾何学の角度の和を返すもので、常に180度より小さくなります。この関数は多くの数理物理学の問題で使われ、特殊相対性理論や一般相対性理論の研究にも登場します。
sinh( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
sqrt (Square Root)
◇記述( Description)
Square root (平方根)関数は実数の平方根をとり、実数を返します。
sqrt( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができ、標準入力変数(Time、Frame、Value)のいずれかを受け入れることができます。
tan (Tangent)
◇記述( Description)
Tangent関数は sine を cosine で割ったものです。Pl/2 のように、その値でオブジェクトが消えてしまうような、ありえない結果にならないように注意してください。
tan( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
tanh (Hyperbolic-Tangent)
◇記述( Description)
Hyperbolic Tangent は通常の tangent とは異なります。これは双曲幾何学の角度の和を返すもので、常に180度より小さくなります。この関数は多くの数理物理学の問題で使われ、特殊相対性理論や一般相対性理論の研究に登場します。
tanh( InputA )
InputA には数値、チャンネル、サブエクスプレッションを指定することができる。
リンク
本記事に戻る